Understanding the Shape of Large-Scale Data

Posted by Anton Tsitsulin, Research Intern and Bryan Perozzi, Senior Research Scientist, Graph Mining Team, Google Research

Understanding the differences and similarities between complex datasets is an interesting challenge that often arises when working with data. One way to formalize this question is to view each dataset as a graph, a mathematical model for how items relate to each other. Graphs are widely used to model relationships between objects — the Internet graph connects pages referencing each other, social graphs link together friends, and molecule graphs connect atoms bonding with each other.

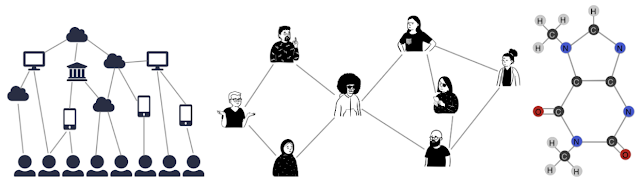Graphs are discrete objects that can model the relationships between many different types of data, including web pages (left), social connections (center), or molecules (right).

Once there is a collection of multiple graphs, it is common to want to predict some property of each one as an aggregate (i.e., one label per graph). For example, consider the task of predicting protein function from structure: each dataset here is one protein, and the prediction task is whether the final structure encodes an enzyme or not. Since one wants a model to actually compute the prediction, we need a representation that lets us generalize across different protein structures. Ideally, one would want a way to represent graphs as vectors without costly labelling. The problem becomes harder with increasing graph size — in the molecule case humans possess some knowledge about their properties, however, reasoning about larger, more complex datasets becomes increasingly difficult.

In this post we highlight some recent advances in the area of graph representation learning with “Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale Graphs” (published at WWW'20), a publication that improves on the scalability of our earlier research, “DDGK: Learning Graph Representations for Deep Divergence Graph Kernels” (published at WWW’19). SLaQ introduces a way to scale computations to approximate a certain class of graph statistics, allowing one to quickly and efficiently characterize large graphs. We are also happy to announce that we have released the code for both papers in the Google Research GitHub repository for graph embeddings.

Fully Unsupervised Learning of Graph Similarity
In our 2019 paper, we showed that it is possible to learn representations for graph similarity with neither domain knowledge nor supervision. We propose deep divergence graph kernels (DDGK), an unsupervised method for learning representations over graphs that encode mappings of similarities between them. Unlike previous work, our unsupervised method jointly learns node representations, graph representations, and an attention-based alignment between graphs.

Here is a t-SNE visualization of the latent representations learned by DDGK to compare proteins. Blue points indicate proteins that encode enzymes and the red points are for those that do not. We can see that the encoding correlates with a structural property of the protein (whether or not it encodes enzymes), even though this context was not provided during training. (Note that this is a projection of the representations, and so the absolute axis values aren’t meaningful.)

In the example above, we demonstrate how these representations can automatically learn to represent graphs and align them in a way that encodes their latent functional similarity. Experiments on other datasets show we can capture similarities and differences across graphs of different types (language, biology, and social interactions).

The pairwise distance between different datasets encoded and aligned using DDGK. Color indicates distance in the latent space, and the scale of similarity ranges from 0 (identical) to 1.0 (very different). We see that the representations can be clustered to group similar datasets together — for example, the datasets nci1 and ptc are both datasets of chemical compounds.

Fast and Accurate Approximation of Spectral Descriptors
A graph’s spectrum is a powerful representation that encodes its properties, including connectivity patterns between graph nodes and clustering information. The spectrum has been shown to convey rich information about the properties of different objects such as the sound of a drum, 3D shapes, graphs, and general high-dimensional data. Applications of spectral graph descriptors include AutoML systems, anomaly detection in dynamic graphs, and chemical molecule characterization.

Currently, learning-based systems such as DDGK do not scale to either large graphs or large graph collections. Alternatively, one can use the spectral information without the learning component to attain more desirable scaling properties. However, computing spectral descriptors for large graphs is computationally prohibitive. Our more recent paper addresses this problem by proposing SLaQ, a method for approximating a family of graph descriptors. Our approach uses a randomized approximation algorithm for computing traces of spectrum functions that allows us to study several well-known spectral graph characteristics like Von Neumann Graph Entropy, Estrada Index, graph energy, and NetLSD.

For example, we use SLaQ to monitor anomalous changes in the Wikipedia graph structure. SLaQ allows us to discern meaningful changes in the structure of the page graph from trivial ones such as mass page renames. Our experiments show two orders of magnitude improvement in approximation accuracy, on average.

Left: The well-known Karate graph represents the social interactions of two martial arts clubs. Right: The spectral descriptors (NetLSD, VNGE, and Estrada Index) computed for the original graph in blue and the version with removed edges in red.

Conclusions
Unsupervised representation learning for graphs is an important problem, and we believe that the methods we highlight here are exciting steps forward in this area! Specifically, SLaQ allows us to compute principled representations for vast datasets, and DDGK introduces a mechanism for automatically learning alignments between datasets. We hope that our contributions will help advance the analysis of large datasets, and will be useful for understanding changes to time-varying graph datasets, like those used in recommendation systems.

Acknowledgements
We thank Marina Munkhoeva, Rami Al-Rfou, and Dustin Zelle who contributed to these works. For more information on the Graph Mining team (part of Algorithm and Optimization Group) visit our pages.